Posted inKeuangan Digital
Refund Aplikasi Dana Panduan Lengkap untuk Pengguna dan Solusi Transaksi
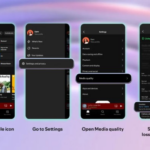
Pernahkah mengalami transaksi yang salah atau merasa dirugikan saat menggunakan aplikasi Dana? Jangan khawatir, karena aplikasi dompet digital ini menyediakan fitur pengembalian dana atau refund. Refund Aplikasi Dana hadir sebagai…